What Is A Graph?
Simply put, a graph is a collection of nodes with edges between them.
* If a node n1 is connected to another node n2 with an edge, we say n1 is adjacent to n2.
그래프는, 각 노드들이 간선들로 서로 연결되어 있는 자료 구조형으로, 아주 커다란 자료 구조형의 범위 중 하나이다.
* Graph > Tree > Linked List 순으로, Graph는 이들을 포괄하고 있는 자료구조형이다.

Graph의 기본 용어 :
Vertex = Node
Edge : 간선.
* 노드와 노드를 연결시켜 주는 역할을 한다.
Graph의 특징 :
- 한 Vertex에서 2개 이상의 노드로 연결이 가능하다.
- 노드 간의 단방향/무방향 경로가 가능하다. Ex. ↔, →
- Self loop, Loop circuit 모두 가능하다.
-Root의 개념이 아니며, 부모와 자식 관계 또한 없다.
- 순환과 비순환으로 나뉜다.
Directed vs Undirected :
Graph 구조는 일방향적인 Edge와 양방향 Edge로 나뉜다.
Directed Graph 예시 : 인스타의 Follow 개념.
- 내가 누군가를 Follow 해도, 상대방이 나를 꼭 Follow 하는 것이 아니다.
Undirected Graph 예시 : 우정, Friendship 개념.

Graph의 더 많은 용어 :
* Adjacent/Neighbors : 인접한.
위의 Undirected Graph에서, A와 B는 인접해있고, A와 C 또한 인접해있다.
그러나, B와 D는 한개의 Edge로 더 연결되있기 때문에 인접해있지 않다.
* Path : 경로
위의 Directed Graph에서, D에서 A로 가는 Path는 없다.
그러나, A에서 D로 가는 경로는 있다. {AC, CD}
* Disconnected graph : 연결되있지 않은 그래프
* Connected graph : 연결되있는 그래프
* Cyclic & Acyclic graph : 시작과 끝이 순환하는 & 순환하지 않는 그래프
* Weighted graph : Edge에 비용이나 거리 등등, 가중치가 할당이 된 그래프.
Adjacency List vs Adjacency Matrix
Adjacency List : 보통 Graph를 나타내는 가장 선호되는 방법이다.
- Node (or Vertex) 가 객체로 저장되어 객체 안에 해당 노드와 인접해있는 모든 노드 리스트를 담는 방법이다.
그러나 가끔, "인접해있는 노드들의 리스트"가 아닌 "Edge들의 리스트"가 사용되기도 한다.
이 경우, "Edge 리스트"는 startNode, endNode 그리고 weight properties(가중치 속성)들을 갖고 있다.
* Adjacency List는 O(n+e) 공간 복잡도를 갖는다.

Adjacency Matrix : n × n of binary values (0 or 1)를 보여주는 Table 형태이다.
* Adjacency Matrix는 O(n²) 공간 복잡도를 갖는다.
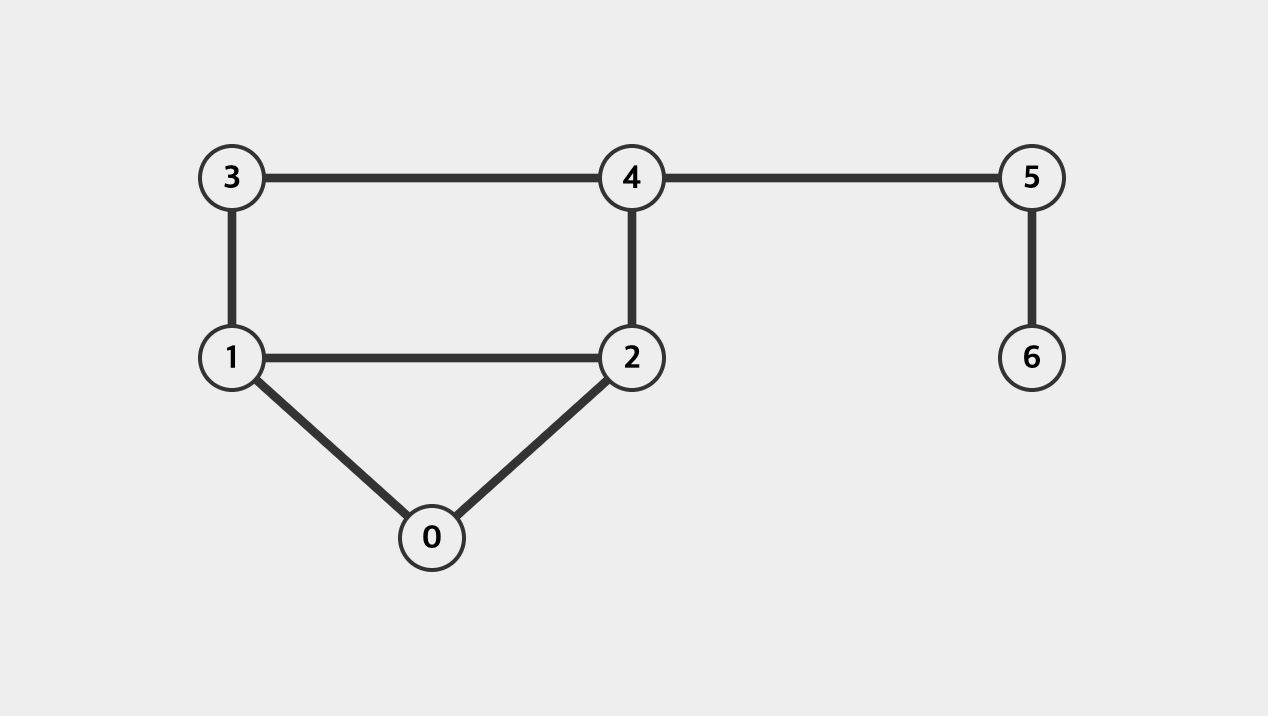

* Adjacency Matrix & Adjacency List & Edge List Visualization을 위한 사이트가 있다.
* 뿐만 아니라, 어렵고도 많은 자료구조를 시각화로 참고해볼 수 있는 사이트니 꼭 북마크하기! → 여기
Graphs - Pros & Cons
장점 : 데이터 간의 관계성
단점 : Scaling is Hard
* 이러한 단점을 상쇄시키기 위해 주로 neo4j 같은 것을 이용해서 만든다고 한다.
'Programming > TIL' 카테고리의 다른 글
| Async & Callback & Promise (0) | 2020.12.21 |
|---|---|
| Data Structure(4) Tree (0) | 2020.12.07 |
| Data Structure(3) Hash Table (0) | 2020.12.04 |
| Data Structure(2) Linked List (0) | 2020.12.04 |
| Big O (0) | 2020.12.03 |



